グリッド細胞の発火パターンをPythonで可視化する
概要
Edvard Moser博士の研究室が公開している、グリッド細胞の活動をPythonで可視化してみました。データはhttps://www.ntnu.edu/kavli/research/grid-cell-dataからダウンロードできます。
コードを書く上でhttp://felix11h.github.io/blog/grid-cell-rate-mapsを参考にしました。一部の関数はこのブログから引用しています。今回は上記のサイトで実装されていない、Gaussian kernelを用いたSmoothed rate mapとAutocorrelation mapの実装をしてみます。
グリッド細胞(Grid Cells)について
実装とは関係ないですが、グリッド細胞についてまとめておきます。
空間基底としてのグリッド細胞
詳しくは場所細胞 - 脳科学辞典や2014年のノーベル生理学・医学賞の解説(神経科学学会)、Grid cells (Scholarpedia)などをお読みいただければと思います。簡単にまとめると、海馬には場所特異的に発火する場所細胞(place cell)があり、これはO'keefe博士によって発見されました。次にMay-Britt Moser博士とEdvard Moser博士は六角形格子状の場所受容野を持つグリッド細胞(格子細胞, grid cell)を内側嗅内皮質(medial entorhinal cortex; MEC)で発見しました。この3人は2014年のノーベル生理学・医学賞を受賞しています。
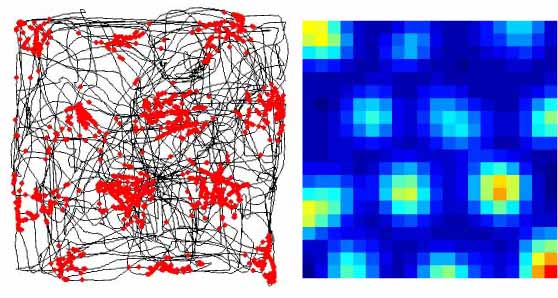
http://www.scholarpedia.org/article/Grid_cellsより。左図の黒線はラットの経路、赤は発火が生じた位置。右図は発火率マップ(rate map)。
最近、外側膝状体背側核(dorsal lateral geniculate nucleus)で場所細胞が見つかったそうです(V Hok, et al., 2018, bioRxiv)。
公開されているデータはMatLabのmatファイル形式です。しかし、scipy.io.loadmatを用いることでpythonでデータの中身を取得することができます。
使用するデータは以下の通りです。
これらのファイルはhttps://archive.norstore.no/pages/public/datasetDetail.jsf?id=8F6BE356-3277-475C-87B1-C7A977632DA7からダウンロードできるファイルの一部です。ただし全体で2.23GBあるので、簡単に試したい場合は上記のリンクからダウンロードしてください。以下では./data/grid_cells_data/ディレクトリの下にファイルを置いています。
データの末尾の"POS"と"T2C3"の意味について説明しておきます。まず、"POS"はpost, posx, posyを含む構造体でそれぞれ試行の経過時間、x座標, y座標です。座標は-50~50で記録されています。恐らく1m四方の正方形の部屋で、原点を部屋の中心としているのだと思います。"T2C3"はtがtetrode(テトロード電極)でcがcell(細胞)を意味します。後ろの数字は番号付けたものと思われます。
Smoothed Rate Mapについて
発火率$\lambda(\boldsymbol{x})$は、場所$\boldsymbol{x}=(x,y)$で記録されたスパイクの回数を、場所$\boldsymbol{x}$における滞在時間(s)で割ることで得られます。 $$ \lambda(\boldsymbol{x})=\frac{\displaystyle \sum_{i=1}^n g\left(\frac{\boldsymbol{s}_i-\boldsymbol{x}}{h}\right)}{\displaystyle \int_0^T g\left(\frac{\boldsymbol{y}(t)-\boldsymbol{x}}{h}\right)dt} $$ ただし、$n$はスパイクの回数、$T$は計測時間、$g(\cdot)$はGaussain Kernel(中身の分子が平均、分母が標準偏差)、$\boldsymbol{s}_i$は$i$番目のスパイクの発生した位置、$\boldsymbol{y}(t)$は時刻$t$でのラットの位置です。分母は積分になっていますが、実際には離散的に記録をするので、累積和に変更し、$dt$を時間のステップ幅(今回は0.02s)とします。
Gaussian Kernelを用いて平滑化することで「10cm四方での発火を同じ位置での発火とする」などとした場合よりも、得られるマップは滑らかになります。
import numpy as np
import matplotlib.pyplot as plt
from scipy import io as io
from tqdm import tqdm
# from http://www.ntnu.edu/kavli/research/grid-cell-data
pos = io.loadmat('./data/grid_cells_data/10704-07070407_POS.mat')
spk = io.loadmat('./data/grid_cells_data/10704-07070407_T2C3.mat')
posファイル内の構造は次のようになっています。
-
pos["post"]: times at which positions were recorded -
pos["posx"]: x positions -
pos["posy"]: y positions -
spk["cellTS"]: spike times
次に種々の関数を実装します。
def nearest_pos(array, value):
k = (np.abs(array - value)).argmin()
return k
def GaussianKernel(sizex, sizey, sigma=0.5, center=None):
"""
sizex : kernel width
sizey : kernel height
sigma : gaussian Sd
center : gaussian mean
return gaussian kernel
"""
x = np.arange(0, sizex, 1, float)
y = np.arange(0, sizey, 1, float)
x, y = np.meshgrid(x,y)
if center is None:
x0 = sizex // 2
y0 = sizey // 2
else:
if np.isnan(center[0])==False and np.isnan(center[1])==False:
x0 = center[0]
y0 = center[1]
else:
return np.zeros((sizey,sizex))
return np.exp(-((x-x0)**2 + (y-y0)**2) / 2*sigma**2)
def smoothed_rate_map(pos, spk, kernel_sigma=0.1,
W=100, H=100):
# load datas
posx = pos["posx"].flatten()
posy = pos["posy"].flatten()
spkt = spk["cellTS"].flatten()
#change positions range: -50 ~ 50 -> 0 ~ H or W
posx = (posx + 50) / 100 * W
posy = (posy + 50) / 100 * H
# find nearest positions when spikes occur
indx = [nearest_pos(pos["post"],t) for t in spkt]
indy = [nearest_pos(pos["post"],t) for t in spkt]
# occup position while trajectory
occup_m_list = []
for i in tqdm(range(len(posx))):
occup_m_list.append(GaussianKernel(W, H, kernel_sigma,
(posx[i], posy[i])))
occup_m = sum(occup_m_list)
occup_m *= 0.02 # one time step is 0.02s
occup_m[occup_m==0] = 1 # avoid devide by zero
# activation
activ_m_list = []
for i in tqdm(range(len(spkt))):
activ_m_list.append(GaussianKernel(W, H, kernel_sigma,
(posx[indx][i] ,posy[indy][i])))
activ_m = sum(activ_m_list)
rate_map = activ_m / occup_m
return rate_map
最後に実行します。
rm = smoothed_rate_map(pos, spk, 0.2, 100, 100)
plt.figure(figsize=(6,4))
plt.imshow(rm, cmap="jet")
plt.colorbar(label="Hz")
plt.gca().invert_yaxis()
plt.tight_layout()
# plt.savefig("smoothed_rate_map.png")
plt.show()
Autocorrelation Mapについて
https://core.ac.uk/download/pdf/30859910.pdfのSupporting Online Materialに書いてある式通りに実装してみましたが、遅い&論文と見た目が全く異なるので、scipy.signal.correlate2dを使いました。
from scipy.signal import correlate2d
rm = smoothed_rate_map(pos, spk, 0.5, 100, 100)
a_corr = correlate2d(rm, rm, fillvalue=5)
plt.figure(figsize=(6,4))
plt.imshow(a_corr, cmap="jet")
plt.colorbar(label="Autocorrelation")
plt.tight_layout()
# plt.savefig("autocorr.png")
plt.show()
若干論文と図が異なる上、cross-correlationが-1~1の範囲でないのはおかしい気がするのですが、六角形格子が見えているので良しとします。