ニューラルネットワークにおける意味発達の数学理論
A. M. Saxe, J. L. McClelland, S. Ganguli. “A mathematical theory of semantic development in deep neural networks”. PNAS. (2019). (arXiv). (PNAS)
を読んだまとめ (+ 実装) です。全部ではなく、初めの部分だけについて解説します。
概要
Abstractからではなく、著者の一人であるS. Ganguli氏のtwitterを日本語訳しました。とりあえず大まかな内容を掴むためのメモのようなものです。
人間の意味的認知における現象が深層ニューラルネットワークでいくつ発生するか、そしてこれらの現象が単純な深層線形ネットワークで解析的に理解されることができるかという研究。
以下は、人間の意味的認知における現象の例。
- 幼児の意味発達に対する概念の階層的な区別。幼児は細かいカテゴリーの区別を取得する前に広いカテゴリーの区別を取得するということである。
- 幼児にはしばらくの間何も学習せず、突然新しい概念を習得するというような発達的学習における段階的な急速な遷移(Rapid stage)が存在する。
- 幼児は発達過程において誤った事実(例えば『芋虫には骨がある』)を思い込んでしまうことがある。そのような事実を裏付けるデータは外部環境には存在しないので、古典的な関連モデルでは説明できない。
- あるカテゴリーの典型的な要素と非典型的な要素の概念(例えば、カナリアは典型的な鳥だがダチョウはそうではない)が存在し、そしてなぜニューラルネットワークが典型的な要素をより迅速に意味的に処理できるのか。
いくつかのカテゴリはより「統一がある(coherent)」(例えば『犬』の集合)ものであり、他のカテゴリはそうではない(例えば『すべてのものが青』の集合)。カテゴリーの統一度(category coherence)の定量的概念を定義し、より統一のあるカテゴリーがより早く学習されることを数学的に証明した。
- 基本レベルの効果:ニューラルネットワークが上位レベル(例えば『動物』)または下位レベル(例えば『ロビン(コマドリなど)』)よりも、基本的な階層レベル(例えば『鳥』)の構造を優先的に学習し、名前付けすることができる理由の説明。
- 発達過程における帰納的一般化のパターンの変化:なぜ幼児やニューラルネットワークは学習の早い段階で過剰に一般化され、その後徐々に一般化のパターンを制限するのかということの説明。
- 表現類似度解析 (Representational Similarity Analysis; RSA):異なる初期重みから同じデータを学習した2つの深層線形ネットワークは、学習が最適(つまり最小ノルム重み)である場合に限り、同じ類似度構造を持つ内部表現を学習する。
知識の獲得とそのダイナミクス
タスク
まずタスクについて。入力 $\boldsymbol{x}$ は「もの」の項目(例えばカナリア、犬、サーモン、樫など)、出力 $\boldsymbol{y}$はそれぞれの項目の性質・特性となっています。例えばカナリア(Canary)は成長し(Grow)、動き(Move)、空を飛べる(Fly)ので、Canaryという入力に対し、ネットワークが出力するのはGrow, Move, Flyとなります。
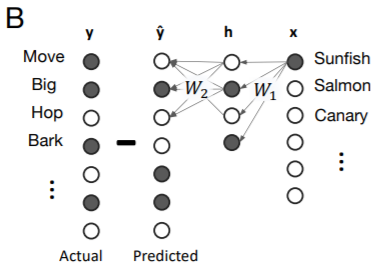
上図はマンボウ(sunfish)の場合です。マンボウはBarkするのでしょうか…。
モデル
モデルは3層の全結合線形ネットワークです。
ただし非線形な活性化関数が無いので、普段使うニューラルネットワークではありません。これはニューラルネットワークを学ぶ人なら誰でも知っていると思いますが、 $ \boldsymbol{ W} ^ {s}={\bf W} ^ {2} \boldsymbol{ W} ^ {1}$として、 上のネットワークは
とまとめることができます。なので線形な活性化関数で深いニューラルネットワークを構築しても何の意味もなく、それゆえ非線形な活性化関数が必要となるということです。しかし、この論文では深い(3層の)ネットワークである場合のみ、幼児の発達における非線形な現象が説明でき、浅い(2層の)ネットワークでは当てはまらないと主張しています。3層で「深い」というのはどうかと思いますが、2層を「浅い」とした場合、比較して「深い」ということです。
学習
ネットワークの学習(重みの更新)は誤差逆伝搬から導かれる次の2式により行います。
ただし、$ \boldsymbol{\Sigma} ^ {x}$は入力間の関係を表す行列、$\boldsymbol{\Sigma} ^ {yx}$は入出力の関係を表す行列です。他にも定義していない変数がありますが、これは後の実装を見ると分かりやすいと思います。
特異値分解(SVD)による学習ダイナミクスの解析
学習ダイナミクスは$ \boldsymbol{\Sigma} ^ {yx}$に対する特異値分解(SVD)を用いて説明できます。
行列$ \boldsymbol{ S}$の対角成分の非ゼロ要素が特異値です。
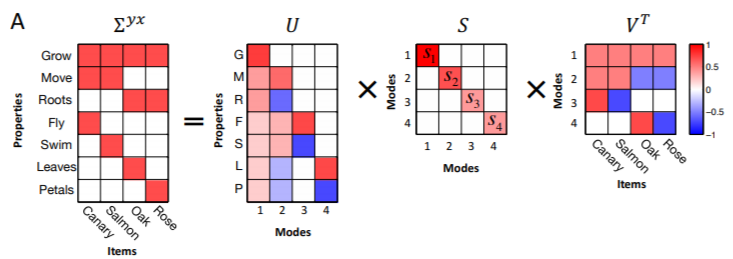
次の図は学習途中における$\hat{\boldsymbol{\Sigma}} ^ {yx}(t)=\boldsymbol{W} ^ 2 (t) \boldsymbol{W} ^ 1(t) \boldsymbol{\Sigma} ^ {x}$のSVDの結果です。$ \boldsymbol{ A}(t)$の要素 $a_{\alpha}(t)$が特異値です。
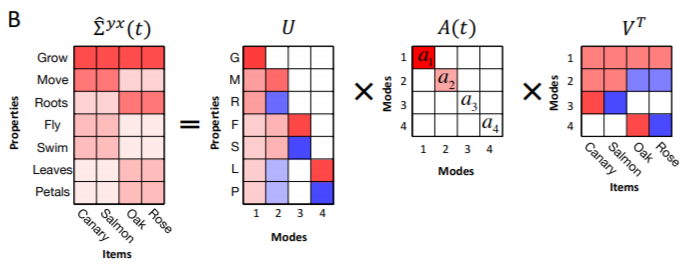
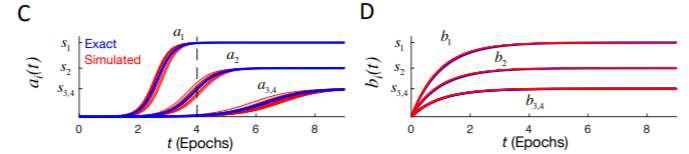
この $a _ {\alpha}(t)$ですが、3層のネットワークの場合、大きな特異値から先に学習されます(C)。2層の浅いネットワークの場合、全ての特異値が同時に学習されます(D)。
このダイナミクスですが、低ランク近似 (low-rank approximation)が生じていて、特異値の大きな要素から学習されていると捉えることができます。学習が進むとランクが大きくなっていく感じです。
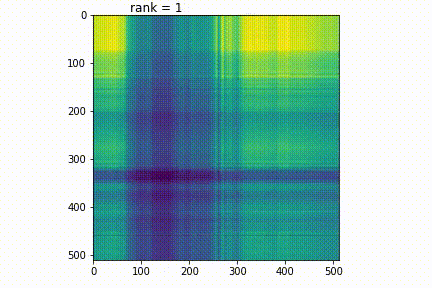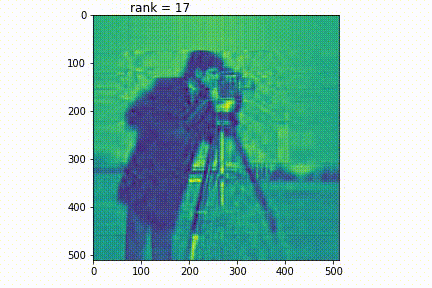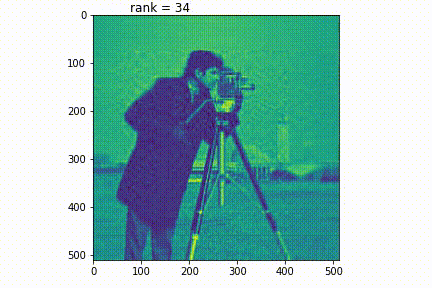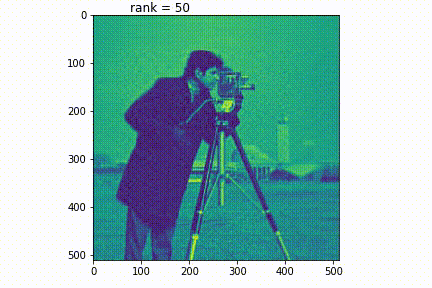
低ランク近似の例として、SVDによる画像の圧縮と復元を見てみましょう。
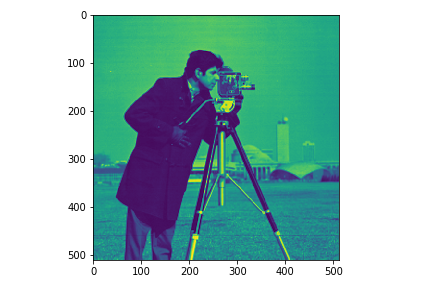
元画像はカメラマンの写真です。この画像に対し、低ランク近似を行い、ランクを上げていきます。するとランクが上がるにつれて、画像が鮮明になります。
from skimage import data
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from tqdm import tqdm
# Low-rank approximation with SVD
def LowRankApprox(u, s, v, rank):
ur = u[:, :rank]
sr = np.diag(s[:rank])
vr = v[:rank, :]
return ur @ sr @ vr
img = data.camera() # 512 x 512
#plt.imshow(img)
#plt.show()
#plt.tight_layout()
#plt.savefig("camera.png")
# Animation
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ims=[]
max_rank = 50
u, s, v = np.linalg.svd(img)
for r in tqdm(range(1, max_rank+1)):
title = fig.text(.3, .97, "rank = "+str(r),
transform = ax.transAxes,
verticalalignment = "center",
fontsize="large")
img_approx = LowRankApprox(u, s, v, rank=r)
im, = [ax.imshow(img_approx)]
ims.append([im, title])
#run animation
ani = animation.ArtistAnimation(fig,ims, interval=500)
plt.tight_layout()
#plt.show()
ani.save("results_video.mp4")
これと同じことが知識の獲得において生じていると見なすことができます。
実装
再現自体は簡単だったので、実装してみました。ニューラルネットワークといえど、numpyで十分なレベルです。一部のハイパーパラメータは適当に設定しています。
3層線形ネットワーク (deep)
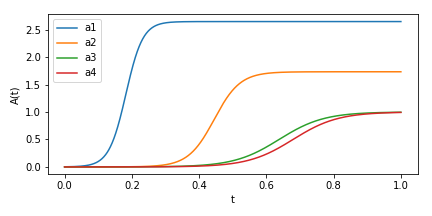
Fig. 3Cに対応。
import numpy as np
import matplotlib.pyplot as plt
# Set initial values
N_1 = 4
N_2 = 16
N_3 = 7
s_yx = np.array([[1,1,1,1],
[1,1,0,0],
[0,0,1,1],
[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1]])
s_x = np.eye(N_1)
u, s, v = np.linalg.svd(s_yx)
eps = 1e-2
w_1 = eps*np.random.rand(N_2,N_1)
w_2 = eps*np.random.rand(N_3,N_2)
# Simulation & training
dt = 0.005
N_t = 1500
A = np.zeros((N_t, N_1))
for t in range(N_t):
# Update
D = s_yx - w_2 @ w_1 @ s_x
dw_1 = (w_2.T @ D) * dt
dw_2 = (D @ w_1.T) * dt
w_1 += dw_1
w_2 += dw_2
# SVD & save results
s_yx_hat = w_2 @ w_1 @ s_x
u, a, v = np.linalg.svd(s_yx_hat)
A[t] += a
# Plot results
T = np.linspace(0.0, 1.0, N_t)
fig = plt.figure(figsize=(6,3))
plt.plot(T, A[:,0], label="a1")
plt.plot(T, A[:,1], label="a2")
plt.plot(T, A[:,2], label="a3")
plt.plot(T, A[:,3], label="a4")
plt.xlabel("t")
plt.ylabel("A(t)")
plt.legend()
plt.tight_layout()
#plt.show()
plt.savefig("result_deep.png")
大きな特異値から学習が始まっているのが分かります。また、それぞれの特異値の学習においてはシグモイド関数様の急速な学習段階が見られます。
2層線形ネットワーク (shallow)
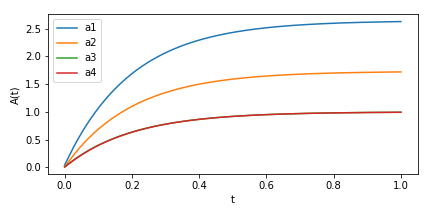
Fig. 3Dに対応。
import numpy as np
import matplotlib.pyplot as plt
# Set initial values
N_1 = 4
#N_2 = 16
N_3 = 7
s_yx = np.array([[1,1,1,1],
[1,1,0,0],
[0,0,1,1],
[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1]])
s_x = np.eye(N_1)
u, s, v = np.linalg.svd(s_yx)
eps = 1e-2
w_s = eps*np.random.rand(N_3,N_1)
# Simulation & training
dt = 0.005
N_t = 1000
A = np.zeros((N_t, N_1))
for t in range(N_t):
# Update
dw_s = (s_yx - w_s @ s_x) * dt
w_s += dw_s
# SVD & save results
s_yx_hat = w_s @ s_x
u, a, v = np.linalg.svd(s_yx_hat)
A[t] += a
# Plot results
T = np.linspace(0.0, 1.0, N_t)
fig = plt.figure(figsize=(6,3))
plt.plot(T, A[:,0], label="a1")
plt.plot(T, A[:,1], label="a2")
plt.plot(T, A[:,2], label="a3")
plt.plot(T, A[:,3], label="a4")
plt.xlabel("t")
plt.ylabel("A(t)")
plt.legend()
plt.tight_layout()
#plt.show()
plt.savefig("result_shallow.png")
全ての特異値の学習が初めから起こっています。ただ、収束はこちらの方が速かったです(パラメータが少ないので)。
考察
学習ダイナミクスにおいて特異値分解が関わっているというのは面白く思いました。ただ、特異値分解自体を学習しているわけではないと思います。
もう1つ面白いと思ったのが知識の混同(例えば『芋虫には骨がある』)の仕組みです。発達において、大きい特異値から先に学習されるため、「動く」、「成長する」などの動物の要素が先に獲得されます。身の回りの動物のほとんどが「骨を持つ」ので、低ランク近似により、『芋虫にも骨がある』と錯覚してしまうのではないか、という話です。
データ数もモデルも小さいので、大きなデータセットに対し、非線形な深層ニューラルネットワークでもこの理論が成り立つのかというのが今後の課題となりそうですね。