話題元はこのツイート

ニューロンの活動を取ってきて並べて表示する場合、ピーク潜時(peak latency)で昇順に並び替え(sort)する場合がある。もちろん主張とは関係のない単なるplotの場合もあるが、その並びに意味があるということを示すためにはちゃんと交差検証して有意かを調べなくてはならない。

というのもsorted plotをすると見る人に与える印象はかなり変わってしまうためである。元ではMATLABだが、全く同じ簡単な実験をPythonで書き直してみる。

プロットの形式による印象の変化

実験としては

  1. bin内のスパイク数を表す(という設定の)行列をランダム(～正規分布)に作成。
  2. ニューロンごとに活動をガウシアンフィルタで平滑化
  3. ピーク潜時に応じて列を並び替え
  4. plotのカラーマップをjetに変更

用いる手順としては他にピーク発火率で正規化(normalization)するというのも入れる場合もあるが、今回は省略。

結果は下図。左から1, 2, 3, 4となっている。

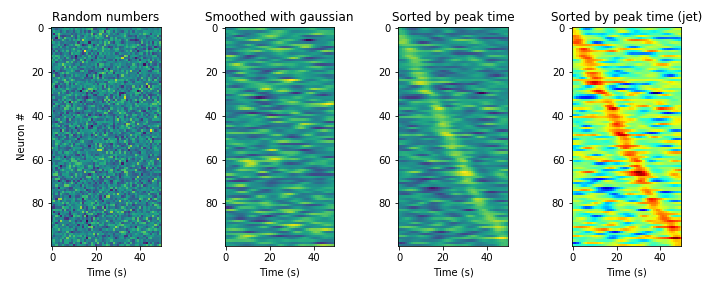
sorted_plot

左端と右端が同じ神経活動を示しているとは思えないほどの変わり方である。不正とは言えないが、見る人に与える印象はとても変わってしまうということに注意しなければならない。

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
 
def GaussianKernel(size, alpha=2.5):
    x = np.arange(0, size, 1, float)
    sigma = (size - 1)/(2*alpha) 
    mu = size // 2
    return np.exp(-((x-mu)**2  / (2*sigma**2)))
 
np.random.seed(seed=1)
N = 100
dt = 1e-2 # sec
T = 0.5 # sec
nt = round(T/dt)
 
# random (number of spikes in dt)
z = np.random.randn(N, nt)
 
# smoothing
kernel = np.expand_dims(GaussianKernel(13), 0)
zs = signal.convolve2d(z, kernel, "same")
 
# sorted plot
max_idx = np.argmax(zs, axis=1)
zs_sorted = zs[np.argsort(max_idx)]
 
 
plt.figure(figsize=(10, 4))
plt.subplot(1,4,1)
plt.imshow(z)
plt.title('Random numbers')
plt.xlabel('Time (s)')
plt.ylabel('Neuron #') 
 
plt.subplot(1,4,2)
plt.imshow(zs)
plt.title('Smoothed with gaussian')
plt.xlabel('Time (s)')
 
plt.subplot(1,4,3)
plt.imshow(zs_sorted)
plt.title('Sorted by peak time')
plt.xlabel('Time (s)')
 
plt.subplot(1,4,4)
plt.imshow(zs_sorted, cmap="jet")
plt.title('Sorted by peak time (jet)')
plt.xlabel('Time (s)')
plt.tight_layout()
#plt.savefig("sorted_plot.png")
plt.show()

smoothingをする場合はkernelを(1, ksize)の行列としてscipyのconvolve2dを用いると速い。

まとめ

このsorted plotの問題はtime cellsの解析において大事なことである。発火潜時で並び替えるとランダムな活動であっても何か意味があるような（＝連鎖的発火が起こっているような）気がしてしまう。そのため適切に統計処理を行わなくてはならない。

関連する話題