Principal Curve（主曲線）

Principal ComponentとPrincipal Curve

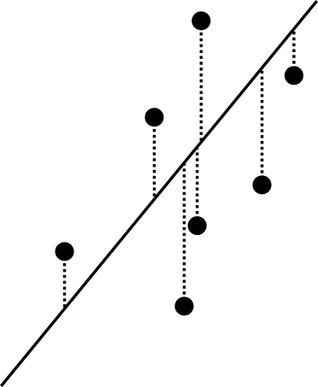
$\boldsymbol{R} ^ d$内で$N$個のデータがどのように分布しているかを，比較的簡単な式で表したい（次元を減らしたい）時がある．一つのよく知られた方法は，線形回帰である．これは，線形関数$f$を用いて，$f(x _ 1,\ldots,\check{x} _ i,\ldots,x _ d)$の式を考え，実際のデータとの差の分散

1N∑k=1N[xi−f(x1,…,xˇi,…,xd)]2\frac{1}{N}\sum _ {k=1} ^ N[x _ i-f(x _ 1,\ldots,\check{x} _ i,\ldots,x _ d)] ^ 2

が最小となるようにする．これは，$\boldsymbol{R} ^ d$内で，$x _ i$軸に沿った，データ点と直線の距離の２乗平均を最小にするのに等しい（図）．

img1

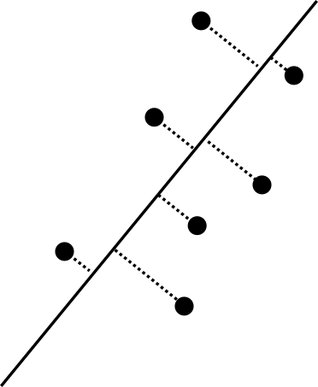
これに対し，主成分分析では，同じく直線を考えるが，その直線に関する成分の２乗和

∑k=1Nx⋅e1\sum _ {k=1} ^ N \boldsymbol{x}\cdot\boldsymbol{e} _ 1

が最大となる単位ベクトル$\boldsymbol{e} _ 1$を方向ベクトルとする直線を第１主成分とする．ここで，各データ点と直線の距離を$d(\boldsymbol{x} _ k)$とすれば，

d(xk)2=∥x∥2−x⋅e1d(\boldsymbol{x} _ k) ^ 2=\|\boldsymbol{x}\| ^ 2-\boldsymbol{x}\cdot\boldsymbol{e} _ 1

なので，主成分分析は各データ点との距離の２乗平均

1N∑k=1Nd(xk)2\frac{1}{N}\sum _ {k=1} ^ N d(\boldsymbol{x} _ k) ^ 2

が最小となるような直線を選ぶことに等しい（図）．

img2

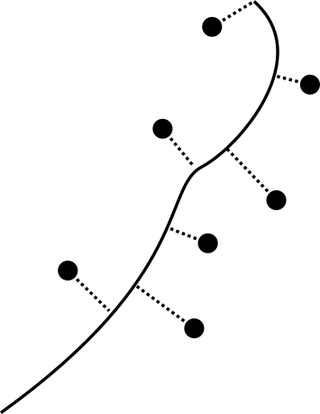
Principal Curve Analysisはデータ点を曲線で代表する方法である．各データ点とその曲線上への射影点との距離の２乗平均が最小となるような曲線を考える（図）.

img3

Principal Curveの定義

$\boldsymbol{R} ^ p$内に確率密度$h$に従って分布した点を$\boldsymbol{X}$で表す．$E(\boldsymbol{X})=0$としても一般性を失わない．$C ^ \infty$級曲線$\boldsymbol{f}:\boldsymbol{R}\supset\Lambda\to\boldsymbol{R} ^ p$を考える．ただし$\boldsymbol{f}$は自己交叉しないものとする：

λ1≠λ2⇒f(λ1)≠f(λ2).\lambda _ 1\neq\lambda _ 2\Rightarrow\boldsymbol{f}(\lambda _ 1)\neq\boldsymbol{f}(\lambda _ 2).

また，パラメータ$\forall\lambda\in\Lambda$について$\boldsymbol{f}$は単位速さであるとする：

∥f′(λ)∥=1.\|\boldsymbol{f}'(\lambda)\|=1.

$\boldsymbol{X}$の$\boldsymbol{f}$に関するprojection index $\lambda _ {\boldsymbol{f}}:\boldsymbol{R} ^ p\to\boldsymbol{R}$を次のように定義する：

λf(x)=sup⁡λ{λ∣∥x−f(λ)∥=inf⁡μ∥x−f(μ)∥}.\lambda _ {\boldsymbol{f}}(\boldsymbol{x})=\sup _ \lambda\left\{\lambda\mid\|\boldsymbol{x}-\boldsymbol{f}(\lambda)\|=\inf _ \mu\|\boldsymbol{x}-\boldsymbol{f}(\mu)\|\right\}.

すなわち，$\boldsymbol{x}$の$\boldsymbol{f}$に関するprojection index $\lambda _ {\boldsymbol{f}}(\boldsymbol{x})$は，$\boldsymbol{x}$に最も近い$\boldsymbol{f}$の点に対応するパラメータのうち最大のものである．

定義A

曲線$\boldsymbol{f}$をself-consistentである，もしくはprincipal curveであるとは，全ての$\lambda\in\Lambda$に対し，

E(X∣λf(X)=λ)=f(λ)E(\boldsymbol{X}\mid\lambda _ {\boldsymbol{f}}(\boldsymbol{X})=\lambda)=\boldsymbol{f}(\lambda)

が成立することである(Hastie and Stuetzle, 1989)．

つまり，projection index $\lambda _ {\boldsymbol{f}}(\boldsymbol{x})$によって$\lambda$に射影される$\boldsymbol{R} ^ p$の全ての点$\boldsymbol{X}$を考える．そのような$\boldsymbol{X}$の平均がちょうど$\boldsymbol{f}(\lambda)$になるのである．

Principal Curveは主成分の自然な拡張である．それは次の定理によって分かる：

定理1

$\boldsymbol{u} _ 0\cdot\boldsymbol{v} _ 0=0$とすると，直線$l(\lambda)=\boldsymbol{u} _ 0+\lambda\boldsymbol{v} _ 0$がself-consistentならば，それは主成分である．

証明

projection indexの性質（最短距離を指すパラメータが複数ある場合は最大値を取る）によって，異なる$\lambda$の原像$\lambda _ {\boldsymbol{f}}{} ^ {-1}(\lambda)$は交わらない．よって，${\boldsymbol{X}}$は，projection indexによって$\lambda$に写る$\boldsymbol{X}$の集合の直和で表される：

{X}=⨁λ{X∣λf(X)=λ}.\{\boldsymbol{X}\}=\bigoplus _ \lambda\{\boldsymbol{X}\mid\lambda _ {\boldsymbol{f}}(\boldsymbol{X})=\lambda\}.

img4

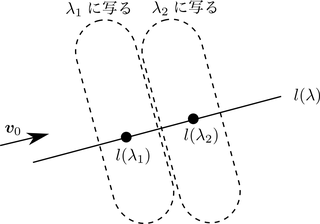
よって，$\boldsymbol{X}$の平均は，ある$\lambda$にprojection indexによって写される$\boldsymbol{X}$の平均$\boldsymbol{X} _ \lambda=E(\boldsymbol{X}\mid\lambda _ {\boldsymbol{f}}(\boldsymbol{X})=\lambda)$の$\lambda$に関する平均に等しい：

0=E(X)=EλE(X∣λf(X)=λ)=Eλ(u0+λv0)=u0+λˉv0.\begin{aligned} 0=E(\boldsymbol{X}) &= E _ \lambda E(\boldsymbol{X}\mid\lambda _ {\boldsymbol{f}}(\boldsymbol{X})=\lambda)\\ &= E _ \lambda(\boldsymbol{u} _ 0+\lambda\boldsymbol{v} _ 0)\\ &= \boldsymbol{u} _ 0+\bar{\lambda}\boldsymbol{v} _ 0. \end{aligned}

両辺$\boldsymbol{u} _ 0$で内積を取れば，$\boldsymbol{u} _ 0\cdot\boldsymbol{v} _ 0=0$なので

u0=0.\boldsymbol{u} _ 0=0.

projection indexによって$\lambda$に写る$\boldsymbol{X}$について$\boldsymbol{u} _ 0$，つまり$l$は原点を通るので，

λf(X)=X⋅v0=Xtv0.\lambda _ {\boldsymbol{f}}(\boldsymbol{X}) = \boldsymbol{X}\cdot\boldsymbol{v} _ 0 = \boldsymbol{X} ^ t\boldsymbol{v} _ 0.

$\boldsymbol{X}$の共分散行列を$\Sigma$とすれば，

Σ=E[(X−E(X))(X−E(X))t]=E(XXt)\Sigma=E\left[(\boldsymbol{X}-E(\boldsymbol{X}))(\boldsymbol{X}-E(\boldsymbol{X})) ^ t\right]=E(\boldsymbol{X}\boldsymbol{X} ^ t)

となるので，

Σv0=E(XXt)v0=EλE(XXtv0∣λf(X)=λ)=EλE(XXtv0∣Xtv0=λ)=EλE(λX∣Xtv0=λ)=Eλλ2v0.\begin{aligned} \Sigma\boldsymbol{v} _ 0 &= E(\boldsymbol{X}\boldsymbol{X} ^ t)\boldsymbol{v} _ 0\\ &= E _ \lambda E(\boldsymbol{X}\boldsymbol{X} ^ t\boldsymbol{v} _ 0\mid\lambda _ {\boldsymbol{f}}(\boldsymbol{X})=\lambda)\\ &= E _ \lambda E(\boldsymbol{X}\boldsymbol{X} ^ t\boldsymbol{v} _ 0\mid\boldsymbol{X} ^ t\boldsymbol{v} _ 0=\lambda)\\ &= E _ \lambda E(\lambda\boldsymbol{X}\mid\boldsymbol{X} ^ t\boldsymbol{v} _ 0=\lambda)\\ &= E _ \lambda\lambda ^ 2\boldsymbol{v} _ 0. \end{aligned}

projection indexの存在

補題2.1

全ての$\boldsymbol{x}\in\boldsymbol{R} ^ p$と$r>0$に対し，集合$Q{\lambda\mid|\boldsymbol{x}-\boldsymbol{f}(\lambda)|\leq r}$はコンパクトである．

証明

$Q$が$\boldsymbol{R} ^ {p}$の有界な閉集合であることが言えれば良い．

$|\boldsymbol{x}-\boldsymbol{f}(\lambda)|$は$\lambda$の連続関数で，値域が閉球体$B ^ \ast(0,r)$であるので，その原像$Q$も閉集合である．

$Q$が有界でないと仮定する．$|\boldsymbol{x}-\boldsymbol{f}(\lambda _ i)|\leq r$を満たす点列$\lambda _ 1,\ldots$が存在する．$B ^ \ast(\boldsymbol{x},2r)$を考える．$\boldsymbol{f}$は$\lambda _ i$から$\lambda _ {i+1}$の間で，ずっと$B ^ \ast(\boldsymbol{x},2r)$の中にあるか，一度$B ^ \ast(\boldsymbol{x},2r)$を出た後，再び入ってくる．何れにせよ，$\boldsymbol{f}$は単位速さであったから，$\boldsymbol{f}(\lambda _ i)$から$\boldsymbol{f}(\lambda _ i{i+1})$までの曲線の長さは少なくとも$\min(2r,\lambda _ {i+1}-\lambda _ i)$である．よって，仮定により${\lambda _ n} _ {n\in\boldsymbol{N}}$が$B(\boldsymbol{x},2r)$内で無限長を持つことになり，矛盾である．

補題2.2

全ての$\boldsymbol{x}\in\boldsymbol{R} ^ p$に対し，$|\boldsymbol{x}-\boldsymbol{f}(\lambda)|=\inf _ {\mu\in\Lambda}|\boldsymbol{x}-\boldsymbol{f}(\mu)|$なる$\lambda\in\Lambda$が存在する．

証明

$r=\inf _ {\mu\in\Lambda}|\boldsymbol{x}-\boldsymbol{f}(\mu)|$，$B={\mu\mid|\boldsymbol{x}-\boldsymbol{f}(\mu)|\leq2r}$とする．$B$は空でなく，コンパクトなので，最大値・最小値が存在する．よって，$\inf _ {\mu\in\Lambda}|\boldsymbol{x}-\boldsymbol{f}(\mu)|=\inf _ {\mu\in B}|\boldsymbol{x}-\boldsymbol{f}(\mu)|$が成立する．

$d(\boldsymbol{x},\boldsymbol{f})=\inf _ {\mu\in\Lambda}|\boldsymbol{x}-\boldsymbol{f}(\mu)|$とする．

定理2

projection index $\lambda _ {\boldsymbol{f}}(\boldsymbol{x})=\sup _ \lambda{\lambda\mid|\boldsymbol{x}-\boldsymbol{f}(\lambda)|=d(\boldsymbol{x},\boldsymbol{f})}$はwell-definedである．

証明

${\lambda\mid|\boldsymbol{x}-\boldsymbol{f}(\lambda)|=d(\boldsymbol{x},\boldsymbol{f})}$は補題\ref{existence _ of _ parameter _ set}から空でなく，補題\ref{compact _ Q}からコンパクトと分かる．

ambiguity pointの集合の測度

補題3.1

$\boldsymbol{x}$の最近点が$\boldsymbol{f}(\lambda _ 0)\ (\lambda _ 0\in\Lambda _ 0)$（ただし，$\lambda _ 0$はパラメータ範囲$\Lambda _ 0$の端点ではないとする）なら，$\boldsymbol{x}$は超平面$(\boldsymbol{x}-\boldsymbol{f}(\lambda _ 0))\cdot\boldsymbol{f}’(\lambda _ 0)$上にある

証明

$\boldsymbol{f}(\lambda _ 0)$は$\boldsymbol{x}$からの距離が最短なので，

0=ddλ∥x−f(λ)∥2∣λ0=−2(x−f(λ0))⋅f′(λ0).\begin{aligned} 0 &= \frac{d}{d\lambda}\|\boldsymbol{x}-\boldsymbol{f}(\lambda)\| ^ 2 \mid _ {\lambda _ 0}\\ &= -2(\boldsymbol{x}-\boldsymbol{f}(\lambda _ 0))\cdot\boldsymbol{f}'(\lambda _ 0). \end{aligned}

定義B

最近点が複数ある（$\text{card}{\lambda\mid|\boldsymbol{x}-\boldsymbol{f}(\lambda)|=d(\boldsymbol{x},\boldsymbol{f})}>1$である）点$\boldsymbol{x}$をambiguity pointと呼ぶ．

$M _ \lambda={\boldsymbol{x}\mid(\boldsymbol{x}-\boldsymbol{f}(\lambda))\cdot\boldsymbol{f}’(\lambda)=0}$とする．補題\ref{hyperplane}から，$\boldsymbol{f}(\lambda)$が$\boldsymbol{x}$の最近点で$\lambda\in\Lambda _ 0$なら$\boldsymbol{x}\in M _ \lambda$である．

全ての$\lambda$について，$\boldsymbol{f}’(\lambda)$と直交するよう$p-1$個のベクトル場$\boldsymbol{n} _ 1(\lambda),\ldots,\boldsymbol{n} _ {p-1}(\lambda)$を考える．$\boldsymbol{\chi}:\Lambda\times\boldsymbol{R} ^ {p-1}\to\boldsymbol{R} ^ p$を次の様に定める：

χ(λ,v)=f(λ)+∑i=1p−1vini(λ).\boldsymbol{\chi}(\lambda,\boldsymbol{v})=\boldsymbol{f}(\lambda)+\sum _ {i=1} ^ {p-1}v _ i\boldsymbol{n} _ i(\lambda).

さらに，$M=\boldsymbol{\chi}(\Lambda,\boldsymbol{R} ^ {p-1})=\bigcup _ \lambda M _ \lambda$を，曲線上の点で，曲線と直交する超平面に属する点の集合とする．

定義C

$X$の部分集合族$\mathcal{F}\in2 ^ X$が$\sigma$加法族であるとは，次の性質を満たすことである：

  1. $A\in\mathcal{F}\Rightarrow A ^ c\in\mathcal{F}$；
  2. $n\in\boldsymbol{N}$に対し，$A _ n\in\mathcal{F}\Rightarrow\bigcup _ {n\in\boldsymbol{N}}A _ n\in\mathcal{F}$．

$\sigma$加法族の定義から直ちに次のことが証明される：

  1. $\phi, X\in\mathcal{F}$．
  2. $n\in\boldsymbol{N}$に対し，$A _ n\in\mathcal{F}\Rightarrow\bigcap _ {n\in\boldsymbol{N}}A _ n\in\mathcal{F}$．
  3. $A,B\Rightarrow A\cup B\in\mathcal{F}$．
  4. $A,B\Rightarrow A\cap B\in\mathcal{F}$．

定義D

$\mathcal{F}$を$X$の$\sigma$加法族とする．$\mu:\mathcal{F}\to\boldsymbol{R}\cup{+\infty}$が測度であるとは次の性質を満たすことである：

  1. $A\in\mathcal{F}$に対し$0\leq\mu(A)\leq+\infty$；
  2. $A _ i,A _ j\in\mathcal{F}\ (i\neq j\in\boldsymbol{N})$に対し，$A _ i\cap A _ j=\varnothing\Rightarrow\mu(\bigcup _ {i\in\boldsymbol{N}}A _ i)=\sum _ {i=1} ^ \infty\mu(A _ i)$．

測度の定義から直ちに次のことが証明される：

  1. $\mu(\varnothing)=0$．
  2. $A,B\in\mathcal{F},\quad A\subset B\Rightarrow \mu(A)\leq\mu(B)$．
  3. $A,B\in\mathcal{F},\quad A\subset B,\quad\mu(B)<+\infty\Rightarrow \mu(B\backslash A)=\mu(B)-\mu(A)$．
  4. $A _ i\in\mathcal{F}\ (i\in\boldsymbol{N})$に対し，$\mu(\bigcup _ {i\in\boldsymbol{N}}A _ i)\leq\sum _ {i=1} ^ \infty\mu(A _ i)$．

補題3.2

$M$に含まれないambiguity pointの（$p$次元）測度は$0$である：$\mu(A\cap M ^ c)$．

証明

$\boldsymbol{x}\in A\cap M ^ c$とする．補題\ref{hyperplane}から，このような点$\boldsymbol{x}$が存在するのは，$\Lambda=[\lambda _ \text{min},\lambda _ \text{max}]$であり，$\boldsymbol{x}$が端点$\boldsymbol{f}(\lambda _ \text{min})$, $\boldsymbol{f}(\lambda _ \text{max})$から等距離にあり，かつそれが曲線$\boldsymbol{f}$との最短である時のみである．これは測度$0$の超平面を形成する．

補題3.3

$E$を測度$0$の集合とする．ambiguity pointの集合$A$の測度が$0$であるためには，$\forall\boldsymbol{x}\in\boldsymbol{R} ^ p\backslash E$に対し，$\mu(A\cap N(\boldsymbol{x}))$なる開近傍$N(\boldsymbol{x})$が存在することが十分である．

証明

開被覆${N(\boldsymbol{x})\mid\boldsymbol{x}\in\boldsymbol{R} ^ p\backslash E}$は明らかに$\bar{A}$を被覆する．$\bar{A}$は$\boldsymbol{R} ^ p$の有界閉集合なのでコンパクトである．よって，${N(\boldsymbol{x})\mid\boldsymbol{x}\in\boldsymbol{R} ^ p\backslash E}$の中から有限個の被覆${N _ i}$を選んで，$A\subset\bar{A}\subset\bigcup _ {i=1} ^ k N _ i$とできる．よって，$\mu(A)\leq\mu(\bigcup _ {i=1} ^ kN _ i\cap A)\leq\sum _ {i=1} ^ {k}\mu(N _ i\cap A)=0$．

補題3.4

$\Lambda$がコンパクトな場合のみ考えても一般性を失わない．

証明

$\Lambda _ n=[-n,n]$, $\boldsymbol{f} _ n=\boldsymbol{f}\mid\Lambda _ n$とし，$A _ n$を$\boldsymbol{f} _ n$のambiguity pointとする．$\boldsymbol{x}$を$\boldsymbol{f}$のambiguity pointとする．補題2.1から${\lambda\mid|\boldsymbol{x}-\boldsymbol{f}(\lambda)|=d(\boldsymbol{x},\boldsymbol{f})}$はコンパクト，つまり$\boldsymbol{R}$の有限閉集合である．

よって，ある$n$が存在し，${\lambda}\in\Lambda _ n$，$\boldsymbol{x}\in A _ n$，$A\subset\bigcup _ {n=1} ^ \infty A _ n$が成立する．ここで，$\mu(A)\leq\mu(\bigcup _ {n=1} ^ \infty A _ n)\leq\sum _ {n=1} ^ \infty\mu(A _ i)$となる．

コンパクトな$\Lambda _ n$を考えて，$\boldsymbol{f} _ n$のambiguity pointの集合$A _ n$について，$\mu(A _ n)=0$を示せばよい．

定義E

写像$f:\boldsymbol{R} ^ m\to\boldsymbol{R} ^ n$について，$\boldsymbol{y}\in\boldsymbol{R} ^ n$が正則値であるとは，$\forall\boldsymbol{x}\in f ^ {-1}(\boldsymbol{y})$について，$f$の微分$f’$の階数が$p$となることである：$\text{rank}(f’(\boldsymbol{x}))=p$．そうでなければ，$\boldsymbol{y}$は臨界値であると言う．

Sardの定理

写像$f:\boldsymbol{R} ^ m\to\boldsymbol{R} ^ n$について$f$の微分可能性が十分高ければ，$f$の臨界値の集合$C$の測度は$0$である．

補題3.5

定義Bで定義した$\boldsymbol{\chi}$の臨界値の集合$C$の測度は$0$である．

証明

$\boldsymbol{\chi}$は$C ^ \infty$級なので，Sardの定理を使う．

定理3

ambiguity pointの集合$A$の測度は$0$である：$\mu(A)=0$．

証明

補題3.4から$\Lambda$がコンパクトの場合のみ考える．補題3.2から$\mu(A\cap M ^ c)=0$．$\boldsymbol{\chi}$の臨界値の集合$C\subset M$を考える．この時，$\mu((A\cap M ^ c)\cup C)=0$なので，補題\ref{measure _ of _ A _ Mc}から，$\forall\boldsymbol{x}\in\boldsymbol{R} ^ p\backslash((A\cap M ^ c)\cup C)=M\backslash C+M ^ c\cap A ^ e$について，$\mu(A\cap N(\boldsymbol{x}))=0$なる近傍$N(\boldsymbol{x})$が存在することを証明すればよい．

$A$の外部$A ^ e$については自明なので，以下では$\forall\boldsymbol{x}\in M\backslash C$（正則値）について，$\mu(A\cap N(\boldsymbol{x}))=0$なる近傍$N(\boldsymbol{x})$が存在することを証明する．

$\boldsymbol{\chi} ^ {-1}\subset\Lambda\times\boldsymbol{R} ^ {p-1}$は有限集合${(\lambda _ 1,\boldsymbol{v _ 1}),\cdots,(\lambda _ k,\boldsymbol{v} _ k)}$である．

仮に，無限集合であったと仮定する．この時，$\boldsymbol{\chi}(\xi _ i,\boldsymbol{w} _ i)=\boldsymbol{x}$を満たす$\Lambda\times\boldsymbol{R} ^ {p-1}$の部分集合${(\xi _ 1,\boldsymbol{w} _ 1),\ldots}$が存在する．$\Lambda$はコンパクト，$\boldsymbol{\chi}$は連続なので，${\xi _ 1,\ldots}$の集積点$\xi _ 0$と対応する$\boldsymbol{w} _ 0$が存在し，$\boldsymbol{\chi}(\xi _ 0,\boldsymbol{w} _ 0)=\boldsymbol{x}$となる．$\boldsymbol{x}$は正則値なので，$\text{rank}(\boldsymbol{\chi}’)=p$である．よって，$(\xi _ 0,\boldsymbol{w} _ 0)$と$\boldsymbol{x}$の近傍で（局所）微分同相になる．よって，これは$\xi _ 0$が集積点であるので矛盾．

$\boldsymbol{\chi}$は正則値なので，$(\lambda _ i,\boldsymbol{v} _ i)$の近傍$L _ i$と$\boldsymbol{x}$の近傍$N(\boldsymbol{x})$で微分同相になる．

この時，$\tilde{N}(\boldsymbol{x})\subset N(\boldsymbol{x})$が存在して，$\boldsymbol{\chi} ^ {-1}(\tilde{N})\subset\bigcup _ {i=1} ^ kL _ i$が成立する．

仮に上記のような$\tilde{N}$が存在しないと仮定する．この時，$\boldsymbol{x}$に収束する点列${\boldsymbol{x} _ i}$が存在し，$(\xi _ i,\boldsymbol{w} _ i)\notin\bigcup _ {i=1} ^ kL _ i$で，$\boldsymbol{\chi}(\xi _ i,\boldsymbol{w} _ i)=\boldsymbol{x} _ i$が成立する．点列${\xi _ i} _ {i\in\boldsymbol{N}}$は集積点$\xi _ 0\in\bigcup _ {i\in\boldsymbol{N}}L _ i$を持つ．しかし，これは$\boldsymbol{\chi}(\xi _ 0,\boldsymbol{w} _ 0)=\boldsymbol{x}$の連続性及び，$\boldsymbol{\chi} ^ {-1}(\boldsymbol{x})$の有限性から矛盾となる．

以上から，$\boldsymbol{y}\in\tilde{N}(\boldsymbol{x})$に対し，$\boldsymbol{\chi}(\lambda _ i(\boldsymbol{y}),\boldsymbol{v} _ i(\boldsymbol{y}))=\boldsymbol{y}$を満たす$(\lambda _ i(\boldsymbol{y}),\boldsymbol{v} _ i(\boldsymbol{y}))$が各$L _ i$に唯一存在する．ここで，$d _ i(\boldsymbol{y})=|\boldsymbol{y}-\boldsymbol{f}(\lambda _ i(\boldsymbol{y}))| ^ 2$とする．補題3.1から，

grad(di(y))=grad∑j=1p[yj−fj(λi(y))]2=(∂∂y1∑j=1p[yj−fj(λi(y))]2,…)=∑j=1p(2[yj−fj(λi(y))]∂∂y1[yj−fj(λi(y))],…)=(∑j=1p2[yj−fj(λi(y))]δ1j,…)−(∑j=1p2[yj−fj(λi(y))]fj′(λi(y))∂λi∂y1,…)=(2[y1−f1(λi(y))],…)−2∂λi∂y1([y−f(λi(y))]⋅f′(λi(y)))=2(y−f(λi(y))).\begin{aligned} \text{grad}(d _ i(\boldsymbol{y})) &= \text{grad}\sum _ {j=1} ^ p[y _ j-f _ j(\lambda _ i(\boldsymbol{y}))] ^ 2\\ &= \left(\frac{\partial}{\partial y _ 1}\sum _ {j=1} ^ p[y _ j-f _ j(\lambda _ i(\boldsymbol{y}))] ^ 2,\ldots \right)\\ &= \sum _ {j=1} ^ p\left(2[y _ j-f _ j(\lambda _ i(\boldsymbol{y}))]\frac{\partial}{\partial y _ 1}[y _ j-f _ j(\lambda _ i(\boldsymbol{y}))],\ldots \right)\\ &= \left(\sum _ {j=1} ^ p2[y _ j-f _ j(\lambda _ i(\boldsymbol{y}))]\delta _ {1j},\ldots\right) -\left(\sum _ {j=1} ^ p2[y _ j-f _ j(\lambda _ i(\boldsymbol{y}))]f ^ \prime _ j(\lambda _ i(\boldsymbol{y}))\frac{\partial\lambda _ i}{\partial y _ 1},\ldots\right)\\ &= \left(2[y _ 1-f _ 1(\lambda _ i(\boldsymbol{y}))],\ldots\right)-2\frac{\partial\lambda _ i}{\partial y _ 1}\left([\boldsymbol{y}-\boldsymbol{f}(\lambda _ i(\boldsymbol{y}))]\cdot\boldsymbol{f}'(\lambda _ i(\boldsymbol{y}))\right)\\ &= 2(\boldsymbol{y}-\boldsymbol{f}(\lambda _ i(\boldsymbol{y}))). \end{aligned}

$\boldsymbol{y}\in\tilde{N}(\boldsymbol{x})$がambiguity pointになるのは，

Aij={z∈N~(x)∣di(z)=dj(z),λi(z)≠λj(z)}A _ {ij} =\{\boldsymbol{z}\in\tilde{N}(\boldsymbol{x})\mid d _ i(\boldsymbol{z})=d _ j(\boldsymbol{z}),\lambda _ i(\boldsymbol{z})\neq\lambda _ j(\boldsymbol{z})\}

として，$\boldsymbol{y}\in A _ {ij}\ (\exists i,j;i\neq j)$の時のみである．

$\boldsymbol{f}$は自己交叉しない（$\eqref{no-self _ crossing$}が成立する）ので，$\lambda _ i(\boldsymbol{z})\neq\lambda _ j(\boldsymbol{z})$ とすると，$\eqref{grad _ d}$から，

grad(di(z)−dj(z))=2(f(λj(z))−f(λi(z)))≠0.\begin{aligned} \text{grad}(d _ i(\boldsymbol{z})-d _ j(\boldsymbol{z})) &= 2(\boldsymbol{f}(\lambda _ j(\boldsymbol{z}))-\boldsymbol{f}(\lambda _ i(\boldsymbol{z})))\\ &\neq0. \end{aligned}

$A _ {ij}$は$p-1$次元多様体であるので，その$p$次元測度は$0$となる：$\mu(A _ {ij})=0$．よって，$\mu(A\cap\tilde{N})=\mu(\bigcup _ {ij}A _ {ij})\leq\sum _ {ij}\mu(A _ {ij})=0$．

bendingアルゴリズム

Principal curveは次のアルゴリズムによって求めることが出来る：

initializaiton

$\boldsymbol{a}$を第１主成分として，$\boldsymbol{f} ^ {0}(\lambda)=\bar{\boldsymbol{x}}+\boldsymbol{a}\lambda$とする．$\lambda ^ {(0)}(\boldsymbol{x})=\lambda _ {\boldsymbol{f} ^ {(0)}}(\boldsymbol{x})=0$とする．

repeat

  1. $\boldsymbol{f} ^ {(j)}(\cdot)=\boldsymbol{E}(\boldsymbol{X}\mid\lambda _ {\boldsymbol{f} ^ {(j-1)}}=\cdot)$とする
  2. $\boldsymbol{f} ^ {(j)}(\lambda)$が単位速さとなるように調整する（曲線の形は変わらない）．
  3. $\lambda ^ {(j)}(\boldsymbol{x})=\lambda _ {\boldsymbol{f} ^ {(j)}}(\boldsymbol{x})\quad\forall\boldsymbol{x}\in h$とする．
  4. $D ^ 2(h,\boldsymbol{f} ^ {(j)})=E _ \lambda E(|\boldsymbol{X}-\boldsymbol{f} ^ {(j)}(\lambda ^ {(j)}(\boldsymbol{X}))| ^ 2\mid\lambda ^ {(j)}(\boldsymbol{X})=\lambda)$を計算する．

until $D ^ 2(h,\boldsymbol{f} ^ {(j)})$がある閾値以下になるまで繰り返す．

これはつまり，点${\boldsymbol{X}}$と曲線の距離の２乗平均が極小値となる曲線を探している．

有限データ点のためのbendingアルゴリズム

$p$次元の$n$個のデータ点を考える．点が有限の場合，principal curveは$(\lambda _ i,\boldsymbol{f} _ i)$の$n$個の集合になる．曲線は単位速さであるとするので，$\lambda _ i$は$\boldsymbol{f} _ 1$から$\boldsymbol{f} _ i$までの折れ線に沿った距離とする．$\lambda _ 1=0$としておく．

まずは，projection index $\lambda _ {\boldsymbol{f} ^ {(j)}}(\boldsymbol{x} _ i)$を求める．$\boldsymbol{x} _ i$と，$\boldsymbol{f} _ k{} ^ {(j)}$と$\boldsymbol{f} _ {k+1}{} ^ {(j)}$を両端とする線分の最短距離を$d _ {ik}$とする．また，$\boldsymbol{f} _ 1{} ^ {(j)}$から最短距離を与える線分側の点までの折れ線に沿った距離を$\lambda _ {ik}$とする．こうして，$1\leq k\leq n-1$に対し$d _ {ik}$と$\lambda _ {ik}$を求める．

img5

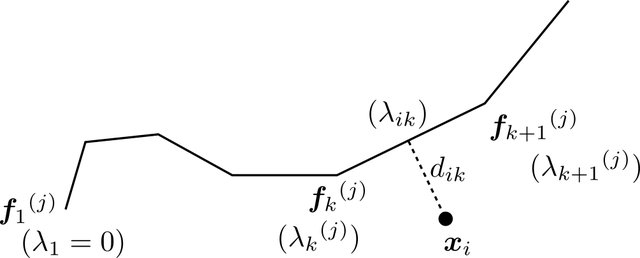
複数データ点のためのprojection index

$\boldsymbol{x} _ i$のprojection index $\lambda _ {i}$は$d _ {ik}$の最小値を与える$\lambda _ {ik}$とする：

λi=λik∗,k∗=argmin⁡1≤k≤n−1dik.\lambda _ {i}=\lambda _ {ik*},\quad k*=\text{arg}\min _ {1\leq k\leq n-1}d _ {ik}.

次に，projection indexが$\lambda _ i$になるような点${\boldsymbol{x}}$の平均を求めて，$\boldsymbol{f} ^ {(j+1)}(\lambda _ i)$（つまり$\boldsymbol{f} _ i{} ^ {(j+1)}$）を構成する．しかし，有限データ点の場合は$\lambda _ i$に投影されるのは$\boldsymbol{x} _ i$唯一という状況がほとんどである．よって，projection index $\lambda _ k$が$\lambda _ i$に近い点${\boldsymbol{x} _ k}$を取ってきて，それらの局所平均を取る(linear weighted running-line smoother)．

$\lambda _ i$に近い$wn\ (0<w<1)$個の$\lambda _ j$及び点${\boldsymbol{x} _ j}$に対し直線を，重み付け最小２乗法でフィッティングする．この際，各重み付けは$\lambda _ i$で最大値を取って，$\lambda _ i$との差が大きいほど$0$に近いもの，例えば，

wij=[1−∣λj−λiλwn th nearest−λi∣3]3w _ {ij} = \left[1- \mid\frac{\lambda _ j-\lambda _ i}{\lambda _ {wn \text{ th nearest}}-\lambda _ i} \mid ^ 3\right] ^ 3

などとする．${\boldsymbol{x} _ j}$の平均は，この直線$\boldsymbol{l}(\lambda)$の$\lambda _ i$での値とする：

fi(j+1)=l(λi).\boldsymbol{f} _ i{} ^ {(j+1)} = \boldsymbol{l}(\lambda _ i).

これによって$n$個の点${\boldsymbol{f} _ i}$が得られる．曲線の長さに従って${\lambda _ {i}{} ^ {(j+1)}}$を定めておく．

k-segmentsアルゴリズム

上に述べたbendingアルゴリズムの他にもPrincipal Curveを求めるアルゴリズムはいくつかあるが，データの曲率が大きかったり，自己交叉があると使い物にならなくなる．それに対処出来るのが，k-segmentsアルゴリズムである(Verbeek, Vlassis, Kr"{o}se, 2001)．

直線$s={\boldsymbol{s}(t)=\boldsymbol{c}+\boldsymbol{u}t\mid t\in\boldsymbol{R}}$を考える．点$\boldsymbol{x}$との距離は d(x,s)=inf⁡t∈R∥s(t)−x∥d(\boldsymbol{x},s)=\inf _ {t\in\boldsymbol{R}}\|\boldsymbol{s}(t)-\boldsymbol{x}\| で定義される．

定義F

$X _ n$を$\boldsymbol{R} ^ d$から取ってきた$n$個のサンプルの集合とする時，Voronoi領域(VR) $V _ 1,\dots,V _ k$を次のように定義する：

Vi={x∈Xn∣i=argmin⁡jd(x,sj)}.V _ i =\{\boldsymbol{x}\in X _ n\mid i=\text{arg}\min _ j d(\boldsymbol{x},s _ j)\}.

つまり，$V _ i$は$i$番目の線$s _ i$が最短となるような$X _ n$の部分集合である．アルゴリズムの目標は全ての点の最短直線との距離の２乗和

∑i=1k∑x∈Vid(x,si)2\sum _ {i=1} ^ k\sum _ {\boldsymbol{x}\in V _ i}d(\boldsymbol{x},s _ i) ^ 2

を最小にするような$k$本の直線$s _ 1,\ldots,s _ k$を見つけることである．

$\eqref{kmeans _ square _ sum}$を最小にするような$k$本の直線を見つけるためには，ランダムな向きと位置にある$k$本の直線を用意して，次のステップを繰り返せば良い：

  1. それぞれの直線についてVRを決定する．
  2. 直線をそれぞれのVRの第１主成分のベクトルで置き換える．

このアルゴリズムが収束することは次のことから分かる：

  • $\eqref{kmeans _ square _ sum}$はVRの定義から，第１ステップで減少する．さらに，主成分の性質から，第２ステップでも減少する．
  • $X _ n$は有限個なので，VRの構成方法は有限である．

ここで，無限に長い直線ではアルゴリズムの計算量が増えるので，線分に限定する．すなわち，アルゴリズムを次のように変える：

  1. それぞれの線分についてVRを決定する．
  2. 線分をそれぞれのVRの第１主成分のベクトルで置き換える．そして，VRのデータ点の第１主成分の分散を$\sigma ^ 2$として，VRの重心から$\frac{3}{2}\sigma$以内の範囲に存在する部分を新しい線分とする．

$k$の決定

$k$を決めるには，$k=1$から初めて，ある条件（線分の上限数やパフォーマンスについての条件など）が満たされるまで増やしていけば良い．

新しい線分の挿入場所を決めるために，各データ点$\boldsymbol{x} _ i$の所に長さ$0$の線分（つまり点$\boldsymbol{c}$）を追加する．この場合，点$\boldsymbol{x}$との最短距離は$d(\boldsymbol{x},s)=|\boldsymbol{x}-\boldsymbol{c}|$で与えられる．よって，この$0$長線分も追加した$k+1$本の成分でVRを構成し，$\eqref{kmeans _ square _ sum}$を計算する．

新しく追加した$0$長線分の中で，$\eqref{kmeans _ square _ sum}$を最も減らすような線分に関するVRを$V _ {k+1}$とする．次に，$V _ {k+1}$での第１主成分のベクトルから，平均からの距離$\frac{3}{2}\sigma$までの線分を作る．これによって$k+1$本の線分が得られた．

有限個の点の集合$S\subset\boldsymbol{R} ^ d$について，平均$\boldsymbol{m}$は２乗距離を最小にする：

m=argmin⁡μ∈Rd∑x∈S∥x−μ∥.\boldsymbol{m}=\text{arg}\min _ {\mu\in\boldsymbol{R} ^ d}\sum _ {\boldsymbol{x}\in S}\|\boldsymbol{x}-\mu\|.

よって，任意の$i$に対し

∑x∈S∥x−m∥2≤∑x∈S∥x−xi∥2.\sum _ {\boldsymbol{x}\in S}\|\boldsymbol{x}-\boldsymbol{m}\| ^ 2\leq\sum _ {\boldsymbol{x}\in S}\|\boldsymbol{x}-\boldsymbol{x} _ i\| ^ 2.

新しい線分$s$は$\boldsymbol{m}$を含むので，$S$内の点から線分への２乗距離和は，$S$内の点から$\boldsymbol{m}$への２乗距離和以下である：

∑x∈Sd(x,s)2≤∑x∈S∥x−m∥2.\sum _ {\boldsymbol{x}\in S}d(\boldsymbol{x},s) ^ 2\leq\sum _ {\boldsymbol{x}\in S}\|\boldsymbol{x}-\boldsymbol{m}\| ^ 2.

よって，線分の挿入による$\eqref{kmeans _ square _ sum}$の減少には下限が存在することが分かる（$V _ {k+1}$を決めた時点で，$\eqref{kmeans _ square _ sum}$の減少は確約されており，以上の式で$S$を$V _ {k+1}$とすれば，そこから更に減少することが言える）．

新しい線分の場所の効率的な探し方

あらかじめ$n$個のデータ間の２乗距離を表す$n\times n$行列$D$を考える：

Dij=∥xi−xj∥2.D _ {ij}=\|\boldsymbol{x} _ i-\boldsymbol{x} _ j\| ^ 2.

各点$\boldsymbol{x} _ i$に対し，最も近い線分までの２乗距離$d _ i ^ \text{VR}$を求めておく．更に

DVR=(d1VRd2VR⋮dnVR),VD=[DVR,…,DVR]\begin{aligned} \boldsymbol{D} ^ \text{VR}= \begin{pmatrix} d _ 1 ^ \text{VR}\\ d _ 2 ^ \text{VR}\\ \vdots\\ d _ n ^ \text{VR} \end{pmatrix},\quad \mathit{VD}=[\boldsymbol{D} ^ \text{VR},\ldots,\boldsymbol{D} ^ \text{VR}] \end{aligned}

とおく．ここで，

Gij=max⁡(VDij−Dij,0)G _ {ij}=\max(\mathit{VD} _ {ij}-D _ {ij},0)

とする．この時$G _ {ij}$は，$0$長線分を$\boldsymbol{x} _ j$に挿入した時の$\boldsymbol{x} _ i$に関する２乗距離の減少に等しい．よって$\eqref{kmeans _ square _ sum}$の減少は$\sum _ iG _ {ij}$に等しいので，

I=(1,…,1)\boldsymbol{I}=(1,\ldots,1)

を考えれば，$0$長線分を$\boldsymbol{x} _ j$に挿入した時の$\eqref{kmeans _ square _ sum}$の減少は$\boldsymbol{I}G$の第$i$成分に等しい．

線分の結合

グラフ$G=(V,E)$を考える．ただし，$V$は$k$本の線分の$2k$個の端点である．更に，$k$本の線分と対応する辺全てを含むような$A\subset E$を考える．全ての頂点を１度ずつつ通過する経路をハミルトニアン経路(HP)と呼ぶ．HPは辺の集合$P\subset E$と考えることができる．線分を結合して多角形のPrincipal Curveを作るために，コストを最小にするようなHP $A\subset P\subset E$（線分に対応する辺を全て含み，かつ全頂点を一度だけ通る経路）を求めたい．経路$P$のコストは

l(P)+λa(P)l(P)+\lambda a(P)

とする．$l(P)$は経路の長さの総和である．辺$e=(v _ i,v _ j)$の長さは

l(e)=∥vi−vj∥l(e)=\|v _ i-v _ j\|

とする．$a(P)$は隣接する角度の和である．$\lambda$を調節することによって，辺の向きが変わることに対するペナルティの重み付けを調節する．

HPを作るためgreedy algorithmで考える．sub-HP $P _ i$と$P _ j$をそれぞれの頂点$v _ i$，$v _ j$で結ぶとする．$e=(v _ i,v _ j)$として，新しくできるsub-HPのコストは元のsub-HPのコストの和と$l(e)+\lambda a(e)$の合計になる．全ての辺$e\in(E\backslash A)$に対し，コスト$c(e)=l(e)+\lambda a(e)$を計算しておく．アルゴリズムは以下のようになる：

  1. k個のsub-HP $A$から始める．
  2. ２個以上のsub-HPがある限り続ける．
  3. $i\neq j$として，２個のsub-HP $P _ i$と$P _ j$を$c(e)$が最小となるような辺$e\in(E-A)$で結ぶ． これによって，折れ線が得られる．

目的関数

最適な$k$を求めるため，データの対数尤度を最大とする折れ線を考える．この折れ線の長さを$l$とし，$\boldsymbol{f}:[0,l]\to\boldsymbol{R} ^ d$で表されるとする．簡単のために，$t\in[0,l]$に対し，$p(t)=\frac{1}{l}$，$p(\boldsymbol{x}\mid t)$は正規分布とする．よって，各データ点の対数尤度への寄与は負号をかけて

−log⁡p(x)=−log⁡∫t∈[0,l]p(x∣t)p(t) dt=log⁡l+c1−log⁡∫t∈[0,l]exp⁡(−∥x−f(t)∥22σ2) dt\begin{aligned} &-\log p(\boldsymbol{x})\\ &= -\log\int _ {t\in[0,l]}p(\boldsymbol{x}\mid t)p(t)\,dt\\ &= \log l+c _ 1-\log\int _ {t\in[0,l]}\exp\left(-\frac{\|\boldsymbol{x}-\boldsymbol{f}(t)\| ^ 2}{2\sigma ^ 2}\right)\,dt \end{aligned}

となる．ここで，図のように距離を取ると，

∥x−f(t)∥2=d⊥(f(t),x)+d∥(f(t),x)=d⊥(s,x)+d∥(f(t),x).\begin{aligned} \|\boldsymbol{x}-\boldsymbol{f}(t)\| ^ 2 &= d _ \perp(\boldsymbol{f}(t),\boldsymbol{x})+d _ \parallel(\boldsymbol{f}(t),\boldsymbol{x})\\ &= d _ \perp(\boldsymbol{s},\boldsymbol{x})+d _ \parallel(\boldsymbol{f}(t),\boldsymbol{x}). \end{aligned}

img6

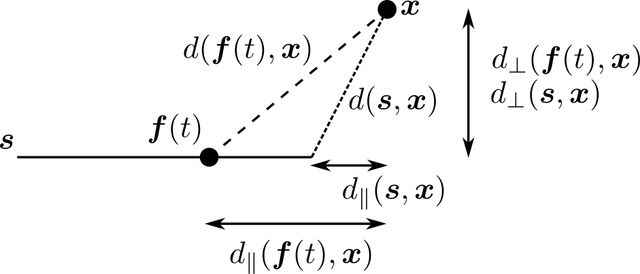
よって，$\eqref{k-segment _ log _ likelihood}$の最後の項は次のように書ける：

d⊥(s,x)22σ2−log⁡∫t∈[0,l]exp⁡(−d∥(f(t),x)22σ2) dt.\frac{d _ \perp(\boldsymbol{s},\boldsymbol{x}) ^ 2}{2\sigma ^ 2}-\log\int _ {t\in[0,l]}\exp\left(-\frac{d _ \parallel(\boldsymbol{f}(t),\boldsymbol{x}) ^ 2}{2\sigma ^ 2}\right)\,dt.

$d _ \parallel(\boldsymbol{s},\boldsymbol{x})=\inf _ {t\in[0,l]}d _ \parallel(\boldsymbol{f}(t),\boldsymbol{x})$とする．$\eqref{k-segment _ log _ likelihood}$は次のように近似できる：

log⁡l+c1+d⊥(s,x)22σ2−log⁡∫exp⁡(−d∥(f(t),x)22σ2) dt∼log⁡l+c1+d⊥(s,x)22σ2−log⁡∫exp⁡(−d∥(s,x)22σ2) dt=log⁡l+d(s,x)22σ2+c.\begin{aligned} &\log l+c _ 1+\frac{d _ \perp(\boldsymbol{s},\boldsymbol{x}) ^ 2}{2\sigma ^ 2}-\log\int\exp\left(-\frac{d _ \parallel(\boldsymbol{f}(t),\boldsymbol{x}) ^ 2}{2\sigma ^ 2}\right)\,dt\\ &\sim\log l+c _ 1+\frac{d _ \perp(\boldsymbol{s},\boldsymbol{x}) ^ 2}{2\sigma ^ 2}-\log\int\exp\left(-\frac{d _ \parallel(\boldsymbol{s},\boldsymbol{x}) ^ 2}{2\sigma ^ 2}\right)\,dt\\ &= \log l + \frac{d(\boldsymbol{s},\boldsymbol{x}) ^ 2}{2\sigma ^ 2} + c. \end{aligned}

よって，全点についての和を取れば，対数尤度に負号をかけたものは

nlog⁡l+∑i=1k∑x∈Vid(si,x)22σ2n\log l+\sum _ {i=1} ^ k\sum _ {\boldsymbol{x}\in V _ i}\frac{d(\boldsymbol{s} _ i,\boldsymbol{x}) ^ 2}{2\sigma ^ 2}

となる．$\eqref{k-segment _ log _ likelihood _ sum}$が初めて極小となる$k$が最適な$k$となる．

参考文献

  • Hastie, T. and Stuetzle, W. (1989). Principal Curves. JASA, 84 (406), 502-516. (pdf)
  • Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. (2nd ed.). Springer. (website)
  • Kegl, B.,Krzyzak, A., Linder, T., and Zeger, K. (2000). Learning and design of principal curves. IEEE. 22 (3), 281-297. (pdf)
  • Verbeek, J., Vlassis, N., and Krose, B. (2002). A k-segments algorithm for finding principal curves. Pattern Recognition Letters, Elsevier. 23 (8), 1009–1017. (pdf)